Direct Standardization

Introduction

Consider a set of observations (xi,yi) drawn non-uniformly from an unknown distribution. We know the expected value of the columns of X, denoted by b∈Rn, and want to estimate the true distribution of y. This situation may arise, for instance, if we wish to analyze the health of a population based on a sample skewed toward young males, knowing the average population-level sex, age, etc. The empirical distribution that places equal probability 1/m on each yi is not a good estimate.

So, we must determine the weights w∈Rm of a weighted empirical distribution, y=yi with probability wi, which rectifies the skewness of the sample (Fleiss, Levin, and Paik 2003, 19.5). We can pose this problem as

maximizew∑mi=1−wilogwisubject tow≥0,∑mi=1wi=1,XTw=b.

Our objective is the total entropy, which is concave on Rm+, and our constraints ensure w is a probability distribution that implies our known expectations on X.

To illustrate this method, we generate m=1000 data points xi,1∼Bernoulli(0.5), xi,2∼Uniform(10,60), and yi∼N(5xi,1+0.1xi,2,1). Then we construct a skewed sample of m=100 points that overrepresent small values of yi, thus biasing its distribution downwards. This can be seen in Figure ???, where the sample probability distribution peaks around y=2.0, and its cumulative distribution is shifted left from the population’s curve. Using direct standardization, we estimate wi and reweight our sample; the new empirical distribution cleaves much closer to the true distribution shown in red.

In the CVXR code below, we import data from the package and solve for w.

## Import problem data
data(dspop)   # Population
data(dssamp)  # Skewed sample

ypop <- dspop[,1]
Xpop <- dspop[,-1]
y <- dssamp[,1]
X <- dssamp[,-1]
m <- nrow(X)

## Given population mean of features
b <- as.matrix(apply(Xpop, 2, mean))

## Construct the direct standardization problem
w <- Variable(m)
objective <- sum(entr(w))
constraints <- list(w >= 0, sum(w) == 1, t(X) %*% w == b)
prob <- Problem(Maximize(objective), constraints)

## Solve for the distribution weights
result <- solve(prob)
weights <- result$getValue(w)
result$value

## [1] 4.223305

We can plot the density functions using linear approximations for the range of y.

## Plot probability density functions
dens1 <- density(ypop)
dens2 <- density(y)
dens3 <- density(y, weights = weights)

## Warning in density.default(y, weights = weights): Selecting bandwidth *not*
## using 'weights'

yrange <- seq(-3, 15, 0.01)
d <- data.frame(x = yrange,
                True = approx(x = dens1$x, y = dens1$y, xout = yrange)$y,
                Sample = approx(x = dens2$x, y = dens2$y, xout = yrange)$y,
                Weighted = approx(x = dens3$x, y = dens3$y, xout = yrange)$y)
plot.data <- gather(data = d, key = "Type", value = "Estimate", True, Sample, Weighted,
                    factor_key = TRUE)
ggplot(plot.data) +
    geom_line(mapping = aes(x = x, y = Estimate, color = Type)) +
    theme(legend.position = "top")

## Warning: Removed 300 rows containing missing values or values outside the scale range
## (`geom_line()`).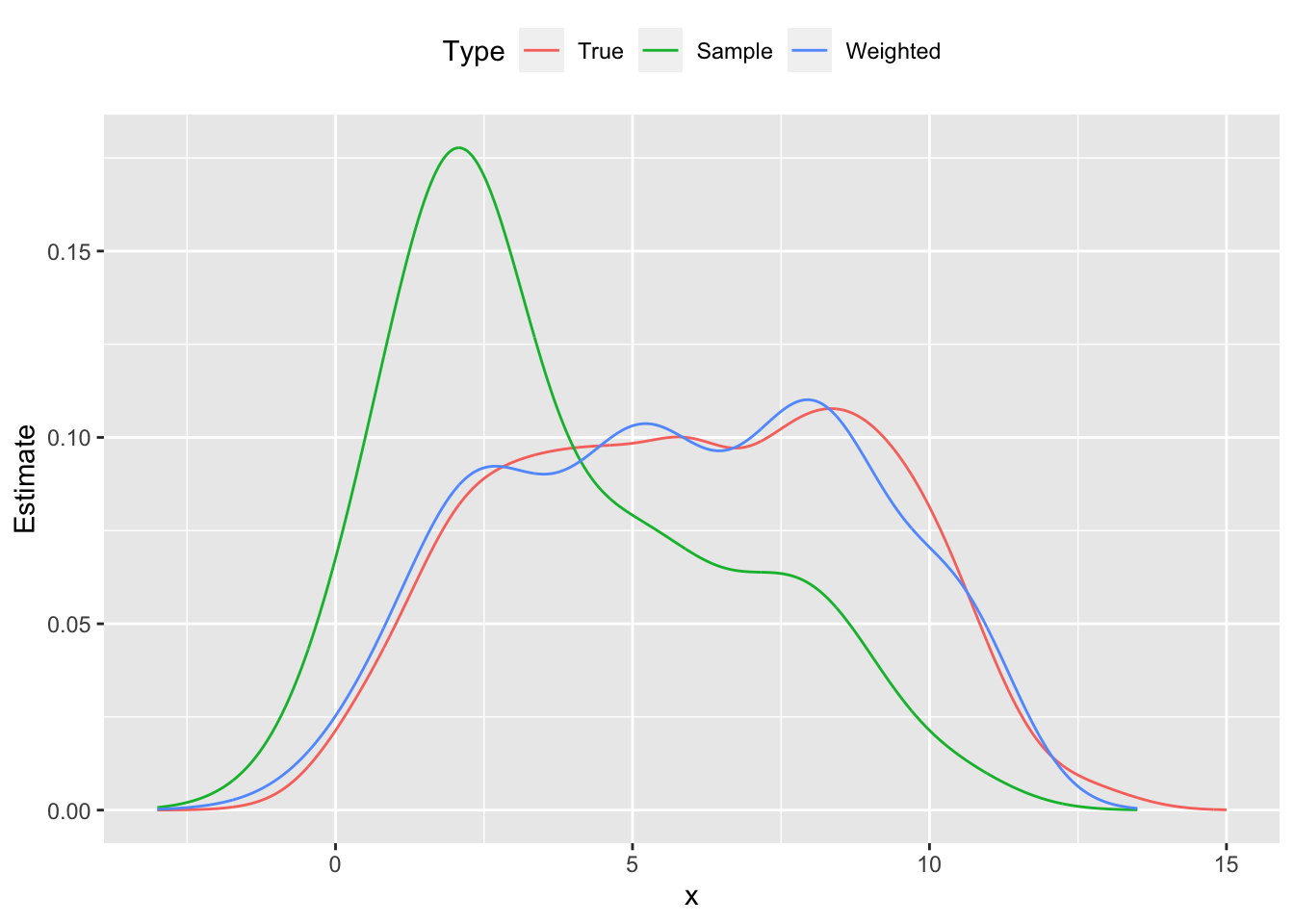

Figure 1: Probability distribution functions population, skewed sample and reweighted sample

Followed by the cumulative distribution function.

## Return the cumulative distribution function
get_cdf <- function(data, probs, color = 'k') {
    if(missing(probs))
        probs <- rep(1.0/length(data), length(data))
    distro <- cbind(data, probs)
    dsort <- distro[order(distro[,1]),]
    ecdf <- base::cumsum(dsort[,2])
    cbind(dsort[,1], ecdf)
}

## Plot cumulative distribution functions
d1 <- data.frame("True", get_cdf(ypop))
d2 <- data.frame("Sample", get_cdf(y))
d3 <- data.frame("Weighted", get_cdf(y, weights))

names(d1) <- names(d2) <- names(d3) <- c("Type", "x", "Estimate")
plot.data <- rbind(d1, d2, d3)

ggplot(plot.data) +
    geom_line(mapping = aes(x = x, y = Estimate, color = Type)) +
    theme(legend.position = "top")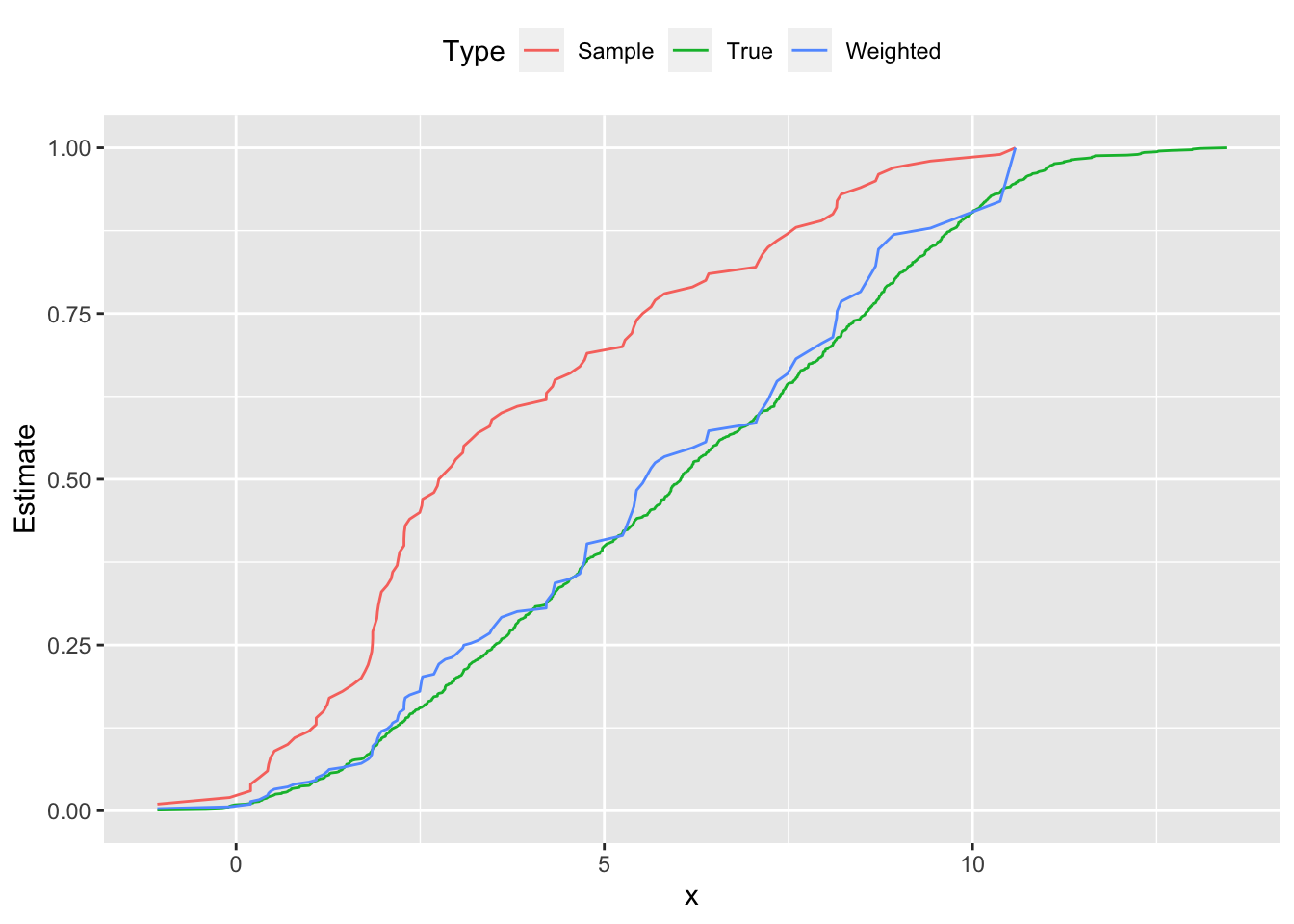

## Testthat Results: No output is good

Session Info

sessionInfo()

## R version 4.4.2 (2024-10-31)
## Platform: x86_64-apple-darwin20
## Running under: macOS Sequoia 15.1
## 
## Matrix products: default
## BLAS:   /Library/Frameworks/R.framework/Versions/4.4-x86_64/Resources/lib/libRblas.0.dylib 
## LAPACK: /Library/Frameworks/R.framework/Versions/4.4-x86_64/Resources/lib/libRlapack.dylib;  LAPACK version 3.12.0
## 
## locale:
## [1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
## 
## time zone: America/Los_Angeles
## tzcode source: internal
## 
## attached base packages:
## [1] stats     graphics  grDevices datasets  utils     methods   base     
## 
## other attached packages:
## [1] tidyr_1.3.1      ggplot2_3.5.1    CVXR_1.0-15      testthat_3.2.1.1
## [5] here_1.0.1      
## 
## loaded via a namespace (and not attached):
##  [1] gmp_0.7-5         clarabel_0.9.0.1  sass_0.4.9        utf8_1.2.4       
##  [5] generics_0.1.3    slam_0.1-54       blogdown_1.19     lattice_0.22-6   
##  [9] digest_0.6.37     magrittr_2.0.3    evaluate_1.0.1    grid_4.4.2       
## [13] bookdown_0.41     pkgload_1.4.0     fastmap_1.2.0     rprojroot_2.0.4  
## [17] jsonlite_1.8.9    Matrix_1.7-1      ECOSolveR_0.5.5   brio_1.1.5       
## [21] Rmosek_10.2.0     purrr_1.0.2       fansi_1.0.6       scales_1.3.0     
## [25] codetools_0.2-20  jquerylib_0.1.4   cli_3.6.3         Rmpfr_0.9-5      
## [29] rlang_1.1.4       Rglpk_0.6-5.1     bit64_4.5.2       munsell_0.5.1    
## [33] withr_3.0.2       cachem_1.1.0      yaml_2.3.10       tools_4.4.2      
## [37] Rcplex_0.3-6      rcbc_0.1.0.9001   dplyr_1.1.4       colorspace_2.1-1 
## [41] gurobi_11.0-0     assertthat_0.2.1  vctrs_0.6.5       R6_2.5.1         
## [45] lifecycle_1.0.4   bit_4.5.0         desc_1.4.3        cccp_0.3-1       
## [49] pkgconfig_2.0.3   bslib_0.8.0       pillar_1.9.0      gtable_0.3.6     
## [53] glue_1.8.0        Rcpp_1.0.13-1     highr_0.11        xfun_0.49        
## [57] tibble_3.2.1      tidyselect_1.2.1  knitr_1.48        farver_2.1.2     
## [61] htmltools_0.5.8.1 labeling_0.4.3    rmarkdown_2.29    compiler_4.4.2

Source

R Markdown