Sparse Inverse Covariance Estimation

Introduction

Assume we are given i.i.d. observations \(x_i \sim N(0,\Sigma)\) for \(i = 1,\ldots,m\), and the covariance matrix \(\Sigma \in {\mathbf S}_+^n\), the set of symmetric positive semidefinite matrices, has a sparse inverse \(S = \Sigma^{-1}\). Let \(Q = \frac{1}{m-1}\sum_{i=1}^m (x_i - \bar x)(x_i - \bar x)^T\) be our sample covariance. One way to estimate \(\Sigma\) is to maximize the log-likelihood with the prior knowledge that \(S\) is sparse (Friedman, Hastie, and Tibshirani 2008), which amounts to the optimization problem:

\[ \begin{array}{ll} \underset{S}{\mbox{maximize}} & \log\det(S) - \mbox{tr}(SQ) \\ \mbox{subject to} & S \in {\mathbf S}_+^n, \quad \sum_{i=1}^n \sum_{j=1}^n |S_{ij}| \leq \alpha. \end{array} \]

The parameter \(\alpha \geq 0\) controls the degree of sparsity. The problem is convex, so we can solve it using CVXR.

Example

We’ll create a sparse positive semi-definite matrix \(S\) using synthetic data

set.seed(1)
n <- 10      ## Dimension of matrix
m <- 1000    ## Number of samples

## Create sparse, symmetric PSD matrix S
A <- rsparsematrix(n, n, 0.15, rand.x = stats::rnorm)
Strue <- A %*% t(A) + 0.05 * diag(rep(1, n))    ## Force matrix to be strictly positive definite

We can now create the covariance matrix \(R\) as the inverse of \(S\).

R <- base::solve(Strue)

As test data, we sample from a multivariate normal with the fact that if \(Y \sim N(0, I)\), then \(R^{1/2}Y \sim N(0, R)\) since \(R\) is symmetric.

x_sample <- matrix(stats::rnorm(n * m), nrow = m, ncol = n) %*% t(expm::sqrtm(R))
Q <- cov(x_sample)    ## Sample covariance matrix

Finally, we solve our convex program for a set of \(\alpha\) values.

Version 1.0 Note: Positive semi-definite variables are now designated using PSD = TRUE rather than the Semidef function!

alphas <- c(10, 8, 6, 4, 1)
if (packageVersion("CVXR") > "0.99-7") {
    S  <- Variable(n, n, PSD = TRUE)
} else {
    S <- Semidef(n)    ## Variable constrained to positive semidefinite cone
}

obj <- Maximize(log_det(S) - matrix_trace(S %*% Q))

S.est <- lapply(alphas,
                function(alpha) {
                    constraints <- list(sum(abs(S)) <= alpha)
                    ## Form and solve optimization problem
                    prob <- Problem(obj, constraints)
                    result <- solve(prob)
                    
                    ## Create covariance matrix
                    R_hat <- base::solve(result$getValue(S))
                    Sres <- result$getValue(S)
                    Sres[abs(Sres) <= 1e-4] <- 0
                    Sres
                })

In the code above, the Semidef constructor restricts S to the positive semidefinite cone. In our objective, we use CVXR functions for the log-determinant and trace. The expression matrix_trace(S %*% Q) is equivalent to `sum(diag(S %*% Q))}, but the former is preferred because it is more efficient than making nested function calls.

However, a standalone atom does not exist for the determinant, so we cannot replace log_det(S) with log(det(S)) since det is undefined for a Semidef object.

## Testthat Results: No output is good

Results

The figures below depict the solutions for the above dataset with \(m = 1000, n = 10\), and \(S\) containing 26% non-zero entries, represented by the dark squares in the images below. The sparsity of our inverse covariance estimate decreases for higher \(\alpha\), so that when \(\alpha = 1\), most of the off-diagonal entries are zero, while if \(\alpha = 10\), over half the matrix is dense. At \(\alpha = 4\), we achieve the true percentage of non-zeros.

do.call(multiplot, args = c(list(plotSpMat(Strue)),
                            mapply(plotSpMat, S.est, alphas, SIMPLIFY = FALSE),
                            list(layout = matrix(1:6, nrow = 2, byrow = TRUE))))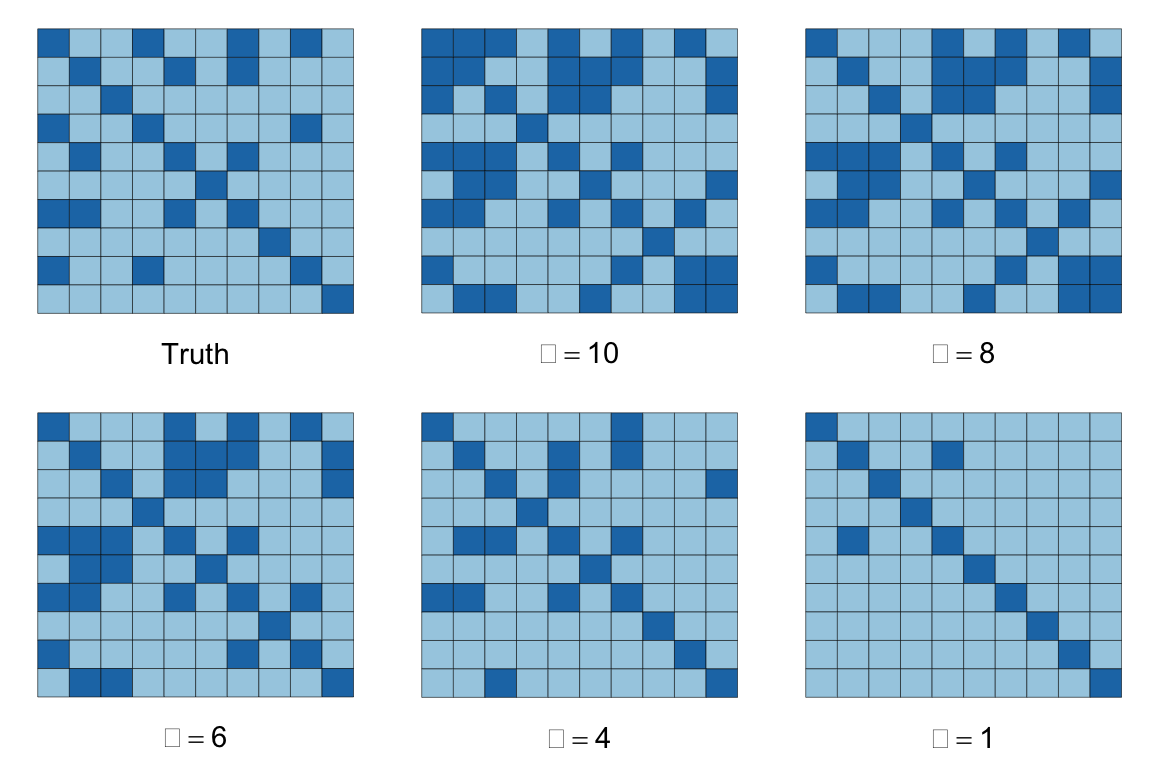

Session Info

sessionInfo()

## R version 4.4.1 (2024-06-14)
## Platform: x86_64-apple-darwin20
## Running under: macOS Sonoma 14.5
## 
## Matrix products: default
## BLAS:   /Library/Frameworks/R.framework/Versions/4.4-x86_64/Resources/lib/libRblas.0.dylib 
## LAPACK: /Library/Frameworks/R.framework/Versions/4.4-x86_64/Resources/lib/libRlapack.dylib;  LAPACK version 3.12.0
## 
## locale:
## [1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
## 
## time zone: America/Los_Angeles
## tzcode source: internal
## 
## attached base packages:
## [1] grid      stats     graphics  grDevices datasets  utils     methods  
## [8] base     
## 
## other attached packages:
## [1] expm_0.999-9     Matrix_1.7-0     ggplot2_3.5.1    CVXR_1.0-15     
## [5] testthat_3.2.1.1 here_1.0.1      
## 
## loaded via a namespace (and not attached):
##  [1] gmp_0.7-4          clarabel_0.9.0     sass_0.4.9         utf8_1.2.4        
##  [5] generics_0.1.3     slam_0.1-50        blogdown_1.19      lattice_0.22-6    
##  [9] digest_0.6.36      magrittr_2.0.3     RColorBrewer_1.1-3 evaluate_0.24.0   
## [13] bookdown_0.40      pkgload_1.4.0      fastmap_1.2.0      rprojroot_2.0.4   
## [17] jsonlite_1.8.8     brio_1.1.5         scs_3.2.4          Rmosek_10.2.0     
## [21] fansi_1.0.6        scales_1.3.0       codetools_0.2-20   jquerylib_0.1.4   
## [25] cli_3.6.3          Rmpfr_0.9-5        rlang_1.1.4        Rglpk_0.6-5.1     
## [29] bit64_4.0.5        munsell_0.5.1      withr_3.0.0        cachem_1.1.0      
## [33] yaml_2.3.9         tools_4.4.1        Rcplex_0.3-6       rcbc_0.1.0.9001   
## [37] dplyr_1.1.4        colorspace_2.1-0   gurobi_11.0-0      assertthat_0.2.1  
## [41] vctrs_0.6.5        R6_2.5.1           lifecycle_1.0.4    bit_4.0.5         
## [45] desc_1.4.3         cccp_0.3-1         pkgconfig_2.0.3    bslib_0.7.0       
## [49] pillar_1.9.0       gtable_0.3.5       glue_1.7.0         Rcpp_1.0.12       
## [53] highr_0.11         xfun_0.45          tibble_3.2.1       tidyselect_1.2.1  
## [57] knitr_1.48         farver_2.1.2       htmltools_0.5.8.1  labeling_0.4.3    
## [61] rmarkdown_2.27     compiler_4.4.1

Source

R Markdown