Largest Ball in a Polyhedron in 2D

Problem

The following is a problem from Boyd and Vandenberghe (2004), section 4.3.1.

Find the largest Euclidean ball (i.e. its center and radius) that lies in a polyhedron described by affine inequalites:

\[ P = {x : a_i'*x <= b_i, i=1,...,m} \]

where x is in \({\mathbf R}^2\).

We define variables that determine the polyhedron.

a1 <- matrix(c(2,1))
a2 <- matrix(c(2,-1))
a3 <- matrix(c(-1,2))
a4 <- matrix(c(-1,-2))
b <- rep(1,4)

Next, we formulate the CVXR problem.

r <- Variable(name = "radius")
x_c <- Variable(2, name = "center")
obj <- Maximize(r)
constraints <- list(
    t(a1) %*% x_c + p_norm(a1, 2) * r <= b[1],
    t(a2) %*% x_c + p_norm(a2, 2) * r <= b[2],
    t(a3) %*% x_c + p_norm(a3, 2) * r <= b[3],
    t(a4) %*% x_c + p_norm(a4, 2) * r <= b[4]
)
p <- Problem(obj, constraints)

All that remains is to solve the problem and read off the solution.

result <- solve(p)
radius <- result$getValue(r)
center <- result$getValue(x_c)
cat(sprintf("The radius is %0.5f for an area %0.5f\n", radius, pi * radius^2))    

## The radius is 0.44721 for an area 0.62832

## Testthat Results: No output is good

A Plot

ggplot() +
    geom_abline(slope = -a1[1] / a1[2], intercept = b[1] / a1[2]) +
    geom_abline(slope = -a2[1] / a2[2], intercept = b[2] / a2[2]) +
    geom_abline(slope = -a3[1] / a3[2], intercept = b[3] / a3[2]) +
    geom_abline(slope = -a4[1] / a4[2], intercept = b[4] / a4[2]) +
    geom_circle(mapping = aes(x0 = center[1], y0 = center[2], r = radius), color = "blue") +
    geom_point(mapping = aes(x = center[1], y = center[2]), color = "red", size = 2) +
    geom_line(mapping = aes(x = c(center[1], center[1] - radius), y = c(center[2], center[2])),
              arrow = arrow(length = unit(0.03, "npc"), ends = "first", type = "closed"),
              color = "brown") +
    annotate("text", x = -0.2, y = 0.04, label = sprintf("r = %0.5f", radius)) +
    labs(x = "x", y = "y") +
    xlim(-1, 1) + ylim(-1, 1)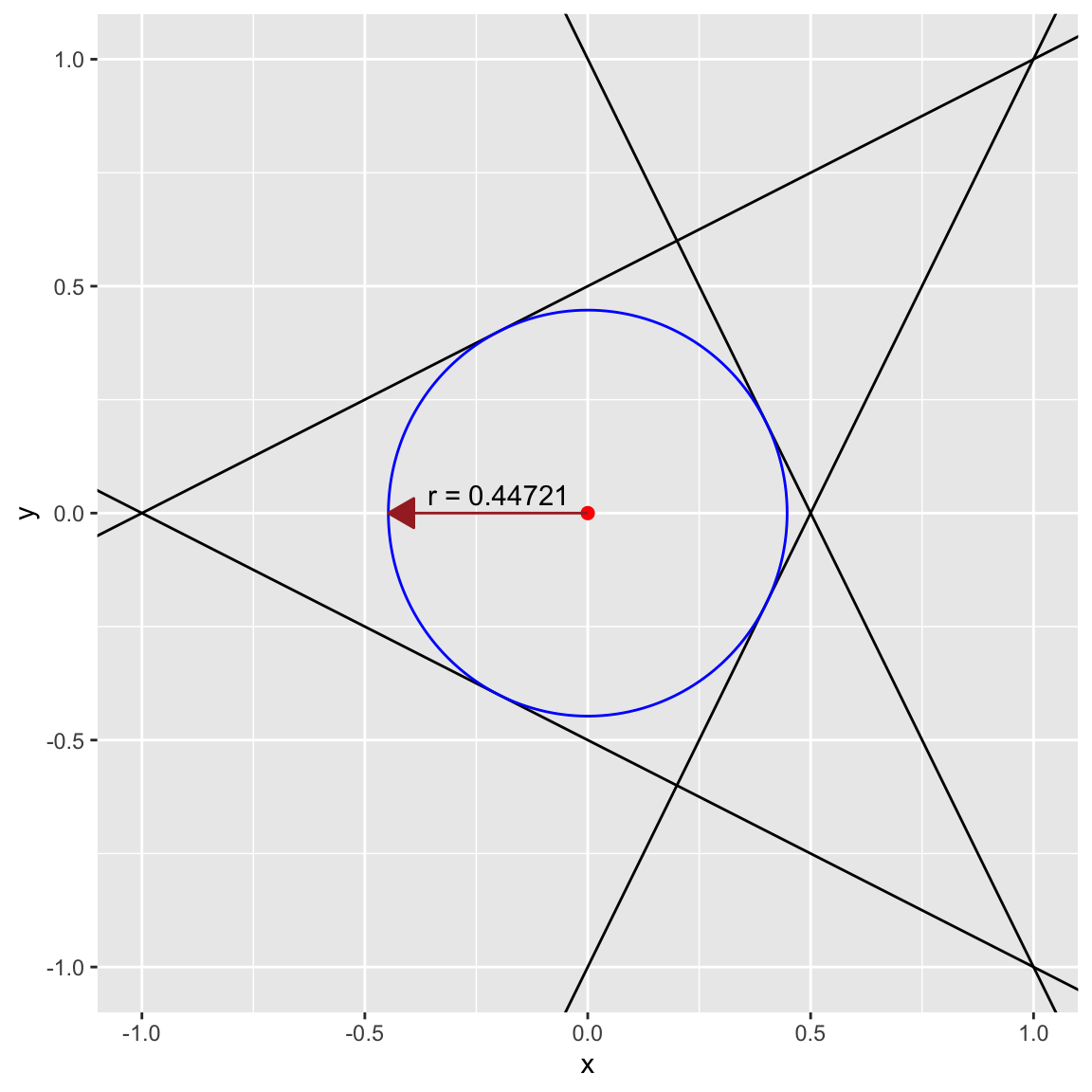

Session Info

sessionInfo()

## R version 4.4.1 (2024-06-14)
## Platform: x86_64-apple-darwin20
## Running under: macOS Sonoma 14.5
## 
## Matrix products: default
## BLAS:   /Library/Frameworks/R.framework/Versions/4.4-x86_64/Resources/lib/libRblas.0.dylib 
## LAPACK: /Library/Frameworks/R.framework/Versions/4.4-x86_64/Resources/lib/libRlapack.dylib;  LAPACK version 3.12.0
## 
## locale:
## [1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
## 
## time zone: America/Los_Angeles
## tzcode source: internal
## 
## attached base packages:
## [1] stats     graphics  grDevices datasets  utils     methods   base     
## 
## other attached packages:
## [1] ggforce_0.4.2    ggplot2_3.5.1    CVXR_1.0-15      testthat_3.2.1.1
## [5] here_1.0.1      
## 
## loaded via a namespace (and not attached):
##  [1] gtable_0.3.5      xfun_0.45         bslib_0.7.0       lattice_0.22-6   
##  [5] vctrs_0.6.5       tools_4.4.1       Rmosek_10.2.0     generics_0.1.3   
##  [9] tibble_3.2.1      fansi_1.0.6       highr_0.11        pkgconfig_2.0.3  
## [13] Matrix_1.7-0      desc_1.4.3        assertthat_0.2.1  lifecycle_1.0.4  
## [17] compiler_4.4.1    farver_2.1.2      brio_1.1.5        munsell_0.5.1    
## [21] gurobi_11.0-0     codetools_0.2-20  htmltools_0.5.8.1 sass_0.4.9       
## [25] cccp_0.3-1        yaml_2.3.9        gmp_0.7-4         pillar_1.9.0     
## [29] jquerylib_0.1.4   MASS_7.3-61       rcbc_0.1.0.9001   Rcplex_0.3-6     
## [33] clarabel_0.9.0    cachem_1.1.0      tidyselect_1.2.1  digest_0.6.36    
## [37] slam_0.1-50       dplyr_1.1.4       bookdown_0.40     labeling_0.4.3   
## [41] polyclip_1.10-6   rprojroot_2.0.4   fastmap_1.2.0     grid_4.4.1       
## [45] colorspace_2.1-0  cli_3.6.3         magrittr_2.0.3    utf8_1.2.4       
## [49] withr_3.0.0       Rmpfr_0.9-5       scales_1.3.0      bit64_4.0.5      
## [53] rmarkdown_2.27    bit_4.0.5         blogdown_1.19     evaluate_0.24.0  
## [57] knitr_1.48        Rglpk_0.6-5.1     rlang_1.1.4       Rcpp_1.0.12      
## [61] glue_1.7.0        tweenr_2.0.3      osqp_0.6.3.3      pkgload_1.4.0    
## [65] jsonlite_1.8.8    R6_2.5.1

Source

R Markdown