L1 Trend Filtering

Introduction

Kim et al. (2009) propose the \(l_1\) trend filtering method for trend estimation. The method solves an optimization problem of the form

\[ \begin{array}{ll} \underset{\beta}{\mbox{minimize}} & \frac{1}{2}\sum_{i=1}^m (y_i - \beta_i)^2 + \lambda ||D\beta||_1 \end{array} \] where the variable to be estimated is \(\beta\) and we are given the problem data \(y\) and \(\lambda\). The matrix \(D\) is the second-order difference matrix,

\[ D = \left[ \begin{matrix} 1 & -2 & 1 & & & & \\ & 1 & -2 & 1 & & & \\ & & \ddots & \ddots & \ddots & & \\ & & & 1 & -2 & 1 & \\ & & & & 1 & -2 & 1\\ \end{matrix} \right]. \]

The implementation is in both C and Matlab. Hadley Wickham provides an R interface to the C code. This is on GitHub and can be installed via:

library(devtools)
install_github("hadley/l1tf")

Example

We will use the example in l1tf to illustrate. The package provides the function l1tf which computes the trend estimate for a specified \(\lambda\).

sp_data <- data.frame(x = sp500$date,
                      y = sp500$log,
                      l1_50 = l1tf(sp500$log, lambda = 50),
                      l1_100 = l1tf(sp500$log, lambda = 100))

The CVXR version

CVXR provides all the atoms and functions necessary to formulat the problem in a few lines. For example, the \(D\) matrix above is provided by the function diff(..., differences = 2). Notice how the formulation tracks the mathematical construct above.

## lambda = 50
y <- sp500$log
lambda_1 <- 50 
beta <- Variable(length(y))
objective_1 <- Minimize(0.5 * p_norm(y - beta) +
                        lambda_1 * p_norm(diff(x = beta, differences = 2), 1))
p1 <- Problem(objective_1)
betaHat_50 <- solve(p1)$getValue(beta)

## lambda = 100
lambda_2 <- 100
objective_2 <- Minimize(0.5 * p_norm(y - beta) +
                        lambda_2 * p_norm(diff(x = beta, differences = 2), 1))
p2 <- Problem(objective_2)
betaHat_100 <- solve(p2)$getValue(beta)

NOTE Of course, CVXR is much slower since it is not optimized just for one problem.

## Testthat Results: No output is good

Comparison Plots

A plot of the estimates for two values of \(\lambda\) is shown below using both approaches. First the l1tf plot.

ggplot(data = sp_data) +
    geom_line(mapping = aes(x = x, y = y), color = 'grey50') +
    labs(x = "Date", y = "SP500 log-price") +
    geom_line(mapping = aes(x = x, y = l1_50), color = 'red', size = 1) +
    geom_line(mapping = aes(x = x, y = l1_100), color = 'blue', size = 1)
## Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
## ℹ Please use `linewidth` instead.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_lifecycle_warnings()` to see where this warning was generated.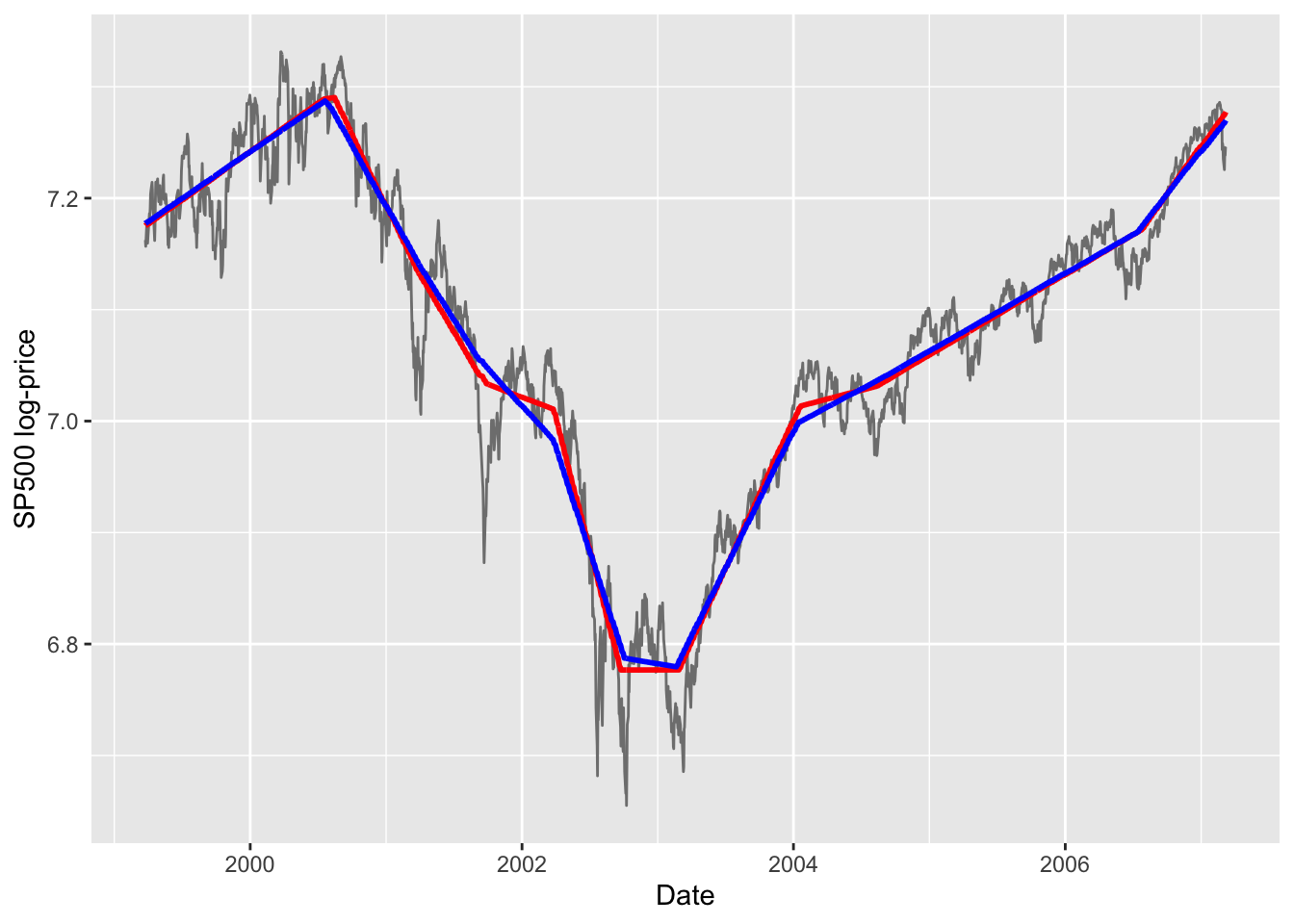
$L_1$ trends for $\lambda = 50$ (red) and $\lambda = 100$ (blue).

Figure 1: \(L_1\) trends for \(\lambda = 50\) (red) and \(\lambda = 100\) (blue).

Next the corresponding CVXR plots.

cvxr_data <- data.frame(x = sp500$date,
                        y = sp500$log,
                        l1_50 = betaHat_50,
                        l1_100 = betaHat_100)
ggplot(data = cvxr_data) +
    geom_line(mapping = aes(x = x, y = y), color = 'grey50') +
    labs(x = "Date", y = "SP500 log-price") +
    geom_line(mapping = aes(x = x, y = l1_50), color = 'red', size = 1) +
    geom_line(mapping = aes(x = x, y = l1_100), color = 'blue', size = 1)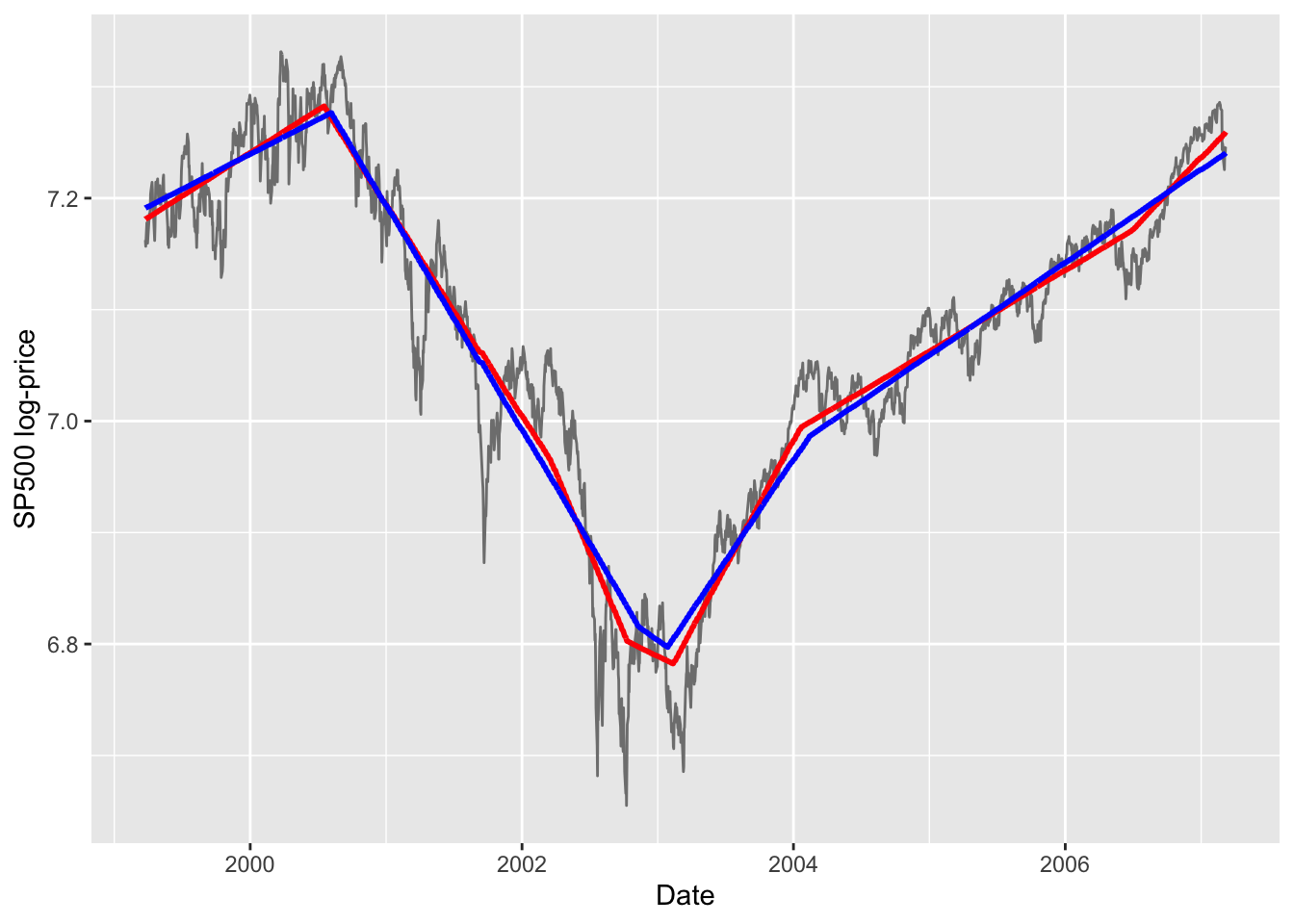
`CVXR` estimated $L_1$ trends for $\lambda = 50$ (red) and $\lambda = 100$ (blue).

Figure 2: CVXR estimated \(L_1\) trends for \(\lambda = 50\) (red) and \(\lambda = 100\) (blue).

Notes

The CVXR solution is not quite exactly that of l1tf: on the left it shows a larger difference for the two \(\lambda\) values; in the middle, it is less flatter than l1tf; and on the right, it does not have as many knots as l1tf.

Session Info

sessionInfo()
## R version 4.4.2 (2024-10-31)
## Platform: x86_64-apple-darwin20
## Running under: macOS Sequoia 15.1
## 
## Matrix products: default
## BLAS:   /Library/Frameworks/R.framework/Versions/4.4-x86_64/Resources/lib/libRblas.0.dylib 
## LAPACK: /Library/Frameworks/R.framework/Versions/4.4-x86_64/Resources/lib/libRlapack.dylib;  LAPACK version 3.12.0
## 
## locale:
## [1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
## 
## time zone: America/Los_Angeles
## tzcode source: internal
## 
## attached base packages:
## [1] stats     graphics  grDevices datasets  utils     methods   base     
## 
## other attached packages:
## [1] l1tf_0.0.0.9000  ggplot2_3.5.1    CVXR_1.0-15      testthat_3.2.1.1
## [5] here_1.0.1      
## 
## loaded via a namespace (and not attached):
##  [1] gmp_0.7-5         clarabel_0.9.0.1  sass_0.4.9        utf8_1.2.4       
##  [5] generics_0.1.3    slam_0.1-54       blogdown_1.19     lattice_0.22-6   
##  [9] digest_0.6.37     magrittr_2.0.3    evaluate_1.0.1    grid_4.4.2       
## [13] bookdown_0.41     pkgload_1.4.0     fastmap_1.2.0     rprojroot_2.0.4  
## [17] jsonlite_1.8.9    Matrix_1.7-1      ECOSolveR_0.5.5   brio_1.1.5       
## [21] Rmosek_10.2.0     fansi_1.0.6       scales_1.3.0      codetools_0.2-20 
## [25] jquerylib_0.1.4   cli_3.6.3         Rmpfr_0.9-5       crayon_1.5.3     
## [29] rlang_1.1.4       Rglpk_0.6-5.1     bit64_4.5.2       munsell_0.5.1    
## [33] withr_3.0.2       cachem_1.1.0      yaml_2.3.10       tools_4.4.2      
## [37] Rcplex_0.3-6      rcbc_0.1.0.9001   dplyr_1.1.4       colorspace_2.1-1 
## [41] gurobi_11.0-0     assertthat_0.2.1  vctrs_0.6.5       R6_2.5.1         
## [45] lifecycle_1.0.4   bit_4.5.0         desc_1.4.3        cccp_0.3-1       
## [49] pkgconfig_2.0.3   bslib_0.8.0       pillar_1.9.0      gtable_0.3.6     
## [53] glue_1.8.0        Rcpp_1.0.13-1     highr_0.11        xfun_0.49        
## [57] tibble_3.2.1      tidyselect_1.2.1  knitr_1.48        farver_2.1.2     
## [61] htmltools_0.5.8.1 labeling_0.4.3    rmarkdown_2.29    compiler_4.4.2

Source

R Markdown

References

Kim, Seung-Jean, Kwangmoo Koh, Stephen Boyd, and Dimitry Gorinevsky. 2009. “\(l_1\) Trend Filtering.” SIAM Review 51 (2): 339–60. https://doi.org/doi:10.1137/070690274.